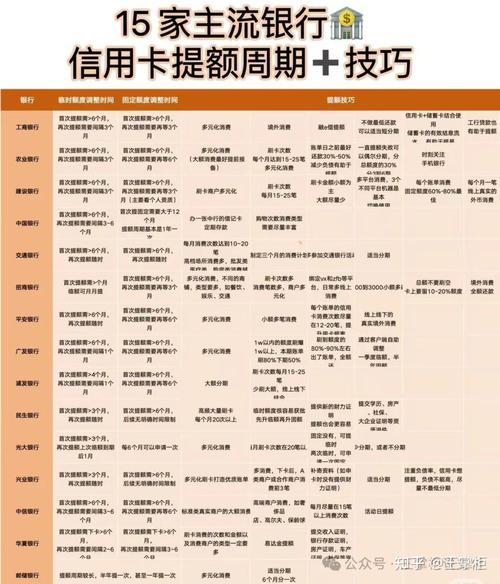
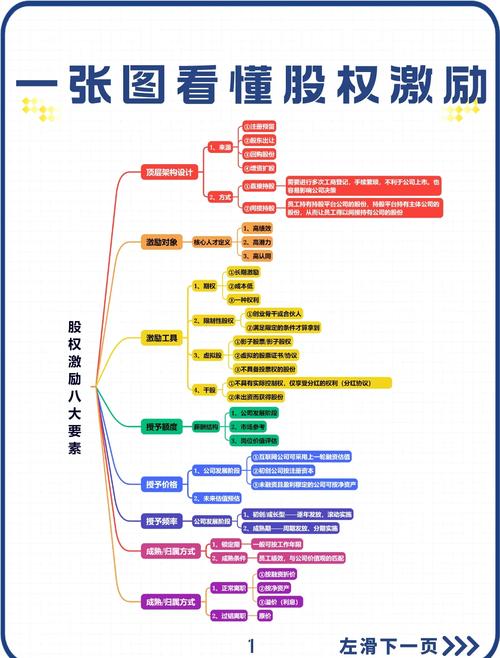
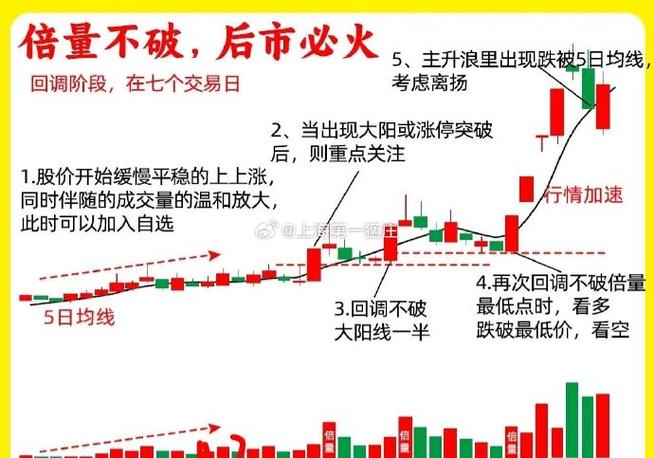
栏目:实盘配资 作者:股票怎么玩 更新:2025-05-18 阅读:174
<股票怎么玩>现金流量图及其绘制:基础概念与作图方法规则全解析

01现金流量图及其绘制
▍ 现金流量图的基础概念
现金流量图是一种用于反映技术方案资金运动状态的图示。通过将技术方案的现金流量以时间坐标图的形式展现,它清晰地展示了各现金流入、流出与相应时间的对应关系。在绘制现金流量图时,需要遵循一定的作图方法和规则,以确保图表的准确性和可读性。
在绘制现金流量图时,我们以横轴作为时间轴,其向右延伸代表时间的持续推进。轴上的每个刻度都代表一个特定的时间单位,如年、半年、季或月等。而时间轴上的每一个点,即称为时点图解货币时间价值系数关系,通常代表该时间单位结束的那一刻。起点则以0表示。
垂直于时间坐标的箭线,代表着在不同时点上的现金流量情况。

需要注意的是,现金流量的性质——即它是流入还是流出,是相对于特定的人而言的。例如,对于投资人来说现金流量图及其绘制:基础概念与作图方法规则全解析,位于横轴上方的箭线表示现金流入,也就是收益;而位于横轴下方的箭线则表示现金流出,也就是费用。
虽然理论上箭线的长短应与现金流量数值的大小成比例,但在实际操作中,由于技术方案中各时点的现金流量往往差异巨大,无法完全按比例绘制。因此,在现金流量图的绘制过程中,只要箭线能够适当反映出各时点现金流量数值的差异,并在箭线上方或下方明确标注出其具体数值即可。箭线与时间轴的交点,正是现金流量实际发生的时点。
▍ 现金流量图的三个关键要素
在绘制现金流量图时现金流量图及其绘制:基础概念与作图方法规则全解析,我们必须紧密把握现金流量的大小(即现金流量数额)、方向(是流入还是流出)以及作用点(现金流量发生的具体时点)。
02终值、现值与等值计算
▍ 一次支付与终值现值转换
描述一次支付系列现金流量,也被称为整存整付,它涉及运用现值与终值的转换关系进行计算。已知现值求终值的公式为:F=P(F/P,i现金流量图及其绘制:基础概念与作图方法规则全解析,n)=P×(1+i)n,而已知终值求现值的公式则为:P=F(P/F,i,n)=F×(1+i)-n。这两个公式是互为逆运算的,它们构成了现值与终值之间的基本转换关系。
▍ 多次支付与年金公式
工程经济中,多次支付即等额支付系列现金流量是一种非常普遍的情况。这种支付方式的特点是现金流量在多个时点上发生,而非集中在单一时点。已知年金求终值的公式为:F=A(F/A,i,n)=A×(1+i)n-1i图解货币时间价值系数关系,而已知年金求现值的公式则为:P=A(P/A,i,n)=A×(1+i)n-1i×(1+i)-n。
此外,我们还可以通过公式推导来理解年金、终值和现值三者之间的相互关系。从P×(1+i)n=A×(1+i)n-1i中图解货币时间价值系数关系,我们可以推导出P=A×(1+i)n-1i(1+i)-n。这进一步证实了三者之间的内在联系和可推导性。
▍ 经典例题分析
在理解这些公式和关系的基础上,我们可以更加熟练地运用它们进行现金流量价值的计算和分析。
例如,某人计划在接下来的5年内,每年年末都向银行存入20万元。假设银行年利率为6%,且按年复利计算,那么他希望在第五年年末能一次性收回所有本金和利息。应用等额年金终值的计算公式可以得出到期可回收的总金额为112.74万元。
另一个例子,某人计划在未来7年内,每年年末都存入固定金额A,并假设年利率为I。他希望了解第8年年末能得到的总金额F的表达式。这涉及到利用年金公式进行现值和终值计算,以便管理多个时点的现金流出或流入。
这一类型的问题和其公式推导过程可以帮助我们更好地理解资金的时间价值及其在工程经济中的实际应用与决策。